重复一篇文献中的模型,来自一篇PRB期刊,题目为Valley-contrasting physics in a two-dimensional px,y-orbital honeycomb lattice,DOI:10.1103/PhysRevB.105.075421

在这篇文章中,用一个很普遍的紧束缚模型来阐述为什么在XYH晶格中的K和K’点会产生谷,以及讨论了两种可行的方法来产生谷极化。
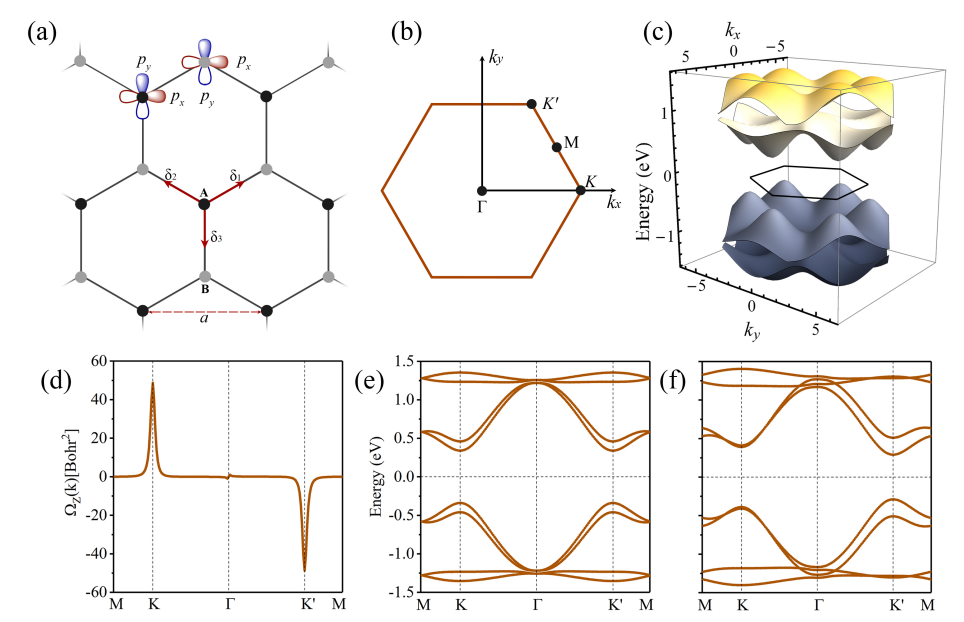
在这个晶格中,每一个格点有两个轨道,分别为px,py,设晶格常数为a
对于这个体系,文章只考虑了最近邻 首先定义两个跃迁系数,分别为t_∥和t_⊥,对于A和B原子,都有三个最近邻,两个原子的在位能项设为相反数
其中,第一个原子的px轨道到第二个原子的px轨道之间的跃迁如下:
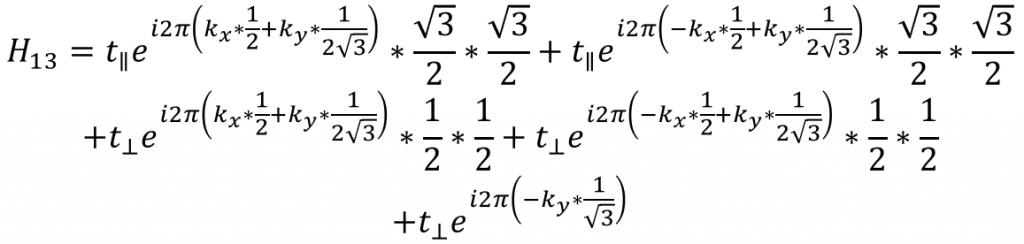
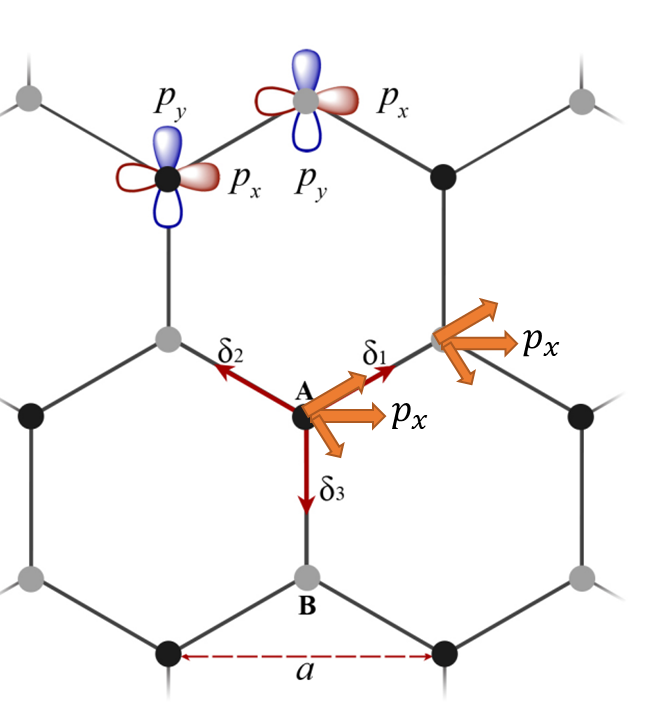
注意A和B如果刚好头碰头则设为t_∥,现在变成了分量
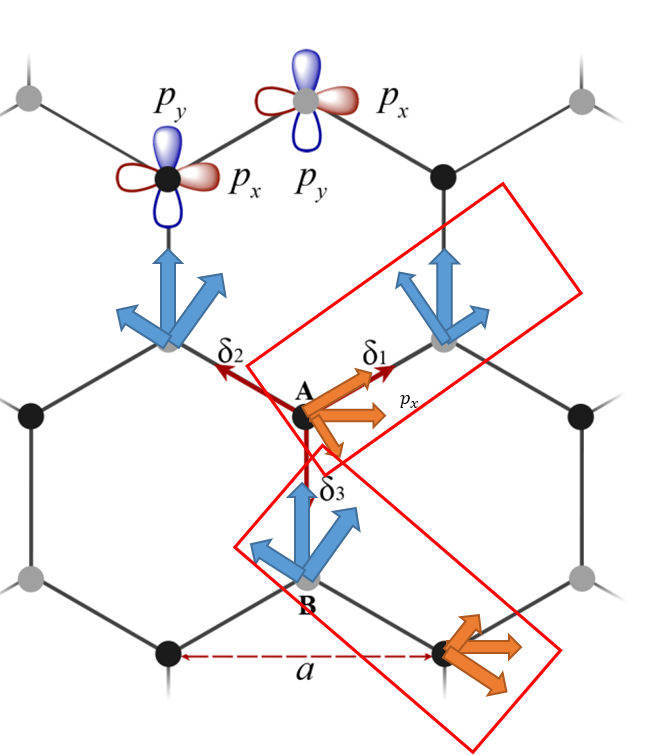
同理,A原子的px到B原子的py的跃迁为
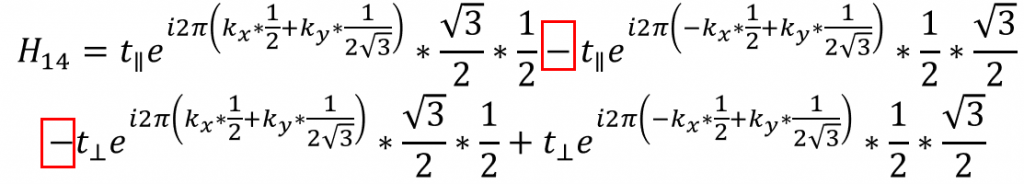
注意这里加了负号,因为这里考虑了头碰头和肩并肩的方向!!!
A原子的py到B原子的px:
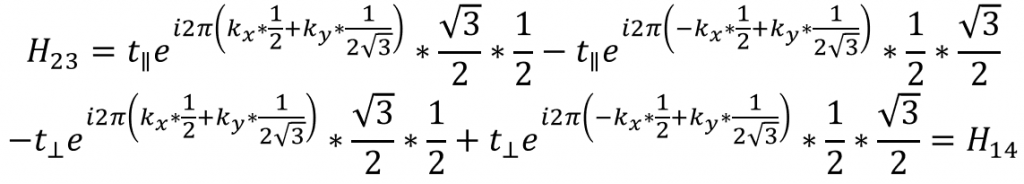
A原子的py到B原子的py:
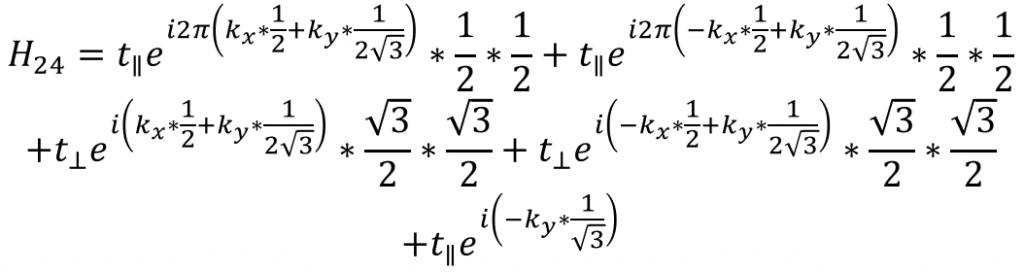
所以总的哈密顿量写成如下形式:
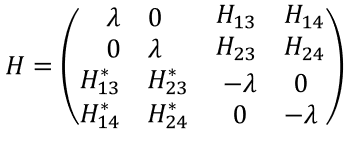









No Comments
Leave a comment Cancel