紧束缚模型（一）

考虑一个双原子分子，每个原子仅有一个轨道，注意这里的波函数与无关，所以只有能级，无法形成能带

此时的哈密顿量为

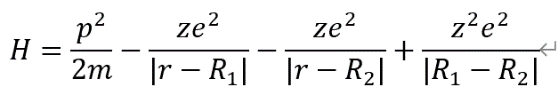
将轨道作用于哈密顿量两端，写成矩阵形式：

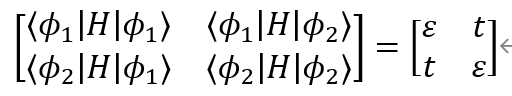
其中

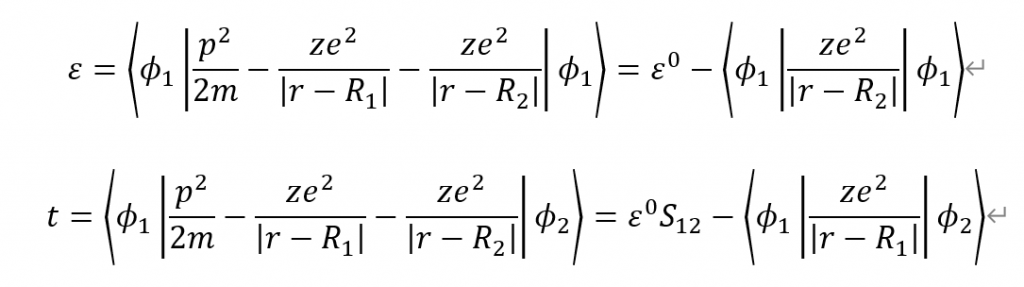
称为交叠矩阵元，一级近似下可以认为恒为0

可解得

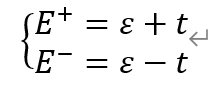
原子轨道线性组合法（linear combination of atomic orbitals）

多体体系的本征波函数可以表示为原子轨道的线性组合：

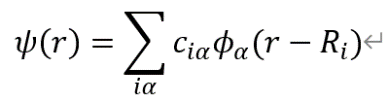
其中i指第i个原胞， 指这个原胞中的轨道

对于具有周期性边界条件的固体体系而言，利用Bloch定理及LOCA方法，我们可以只关注某一个单胞，即利用这一个单胞中原子的波函数及倒空间的矢量k来构建哈密顿量的基函数：

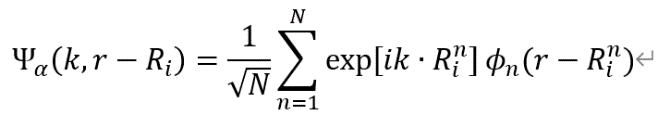
在某一个单胞中，波函数又是上述波函数的组合：

假设原胞中有两个原子，

作用于晶体的哈密顿量上：

将上式左乘

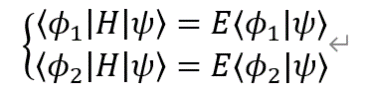
化简

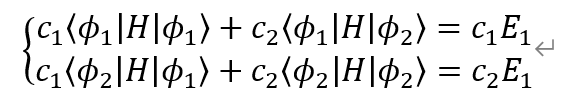
写成矩阵形式

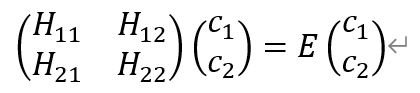
由于正交归一性

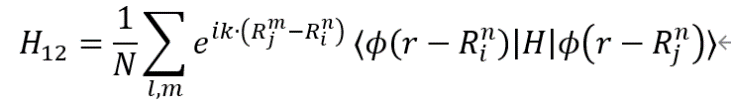
由于N和考虑的近邻数有关，所以最后可以消去。可以令

上式化为

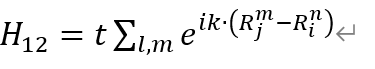
下面是word文件，可供下载