计算陈数

定义某一条能带的陈数

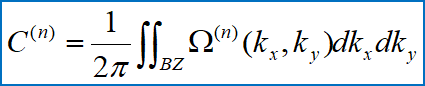
其中，

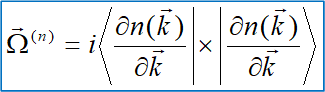
霍尔电导为

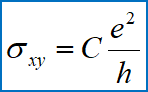
完整代码如下：

from math import *
import math
import sys
from ReadEIGENVAL import *
from numpy import *

import matplotlib.pyplot as pl

# init K vector of random value

num = 4
knum = 239

lat_constant = 1

Ham = [[0 for i in range(num)] for j in range(num)]

lmd = 0.2
t_bot = 1.4
t_parallel = -0.3
# lmd = 0.40669955
# t_bot = 1.32016265
# t_parallel = -0.38963196


def H(kx, ky):
    # lattice
    Ham[0][0] = lmd
    Ham[0][1] = 0
    Ham[0][2] = t_parallel*exp(complex(0, (kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(3/4)+t_parallel*exp(complex(0, (-kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(3/4)+t_bot*exp(
        complex(0, (kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(1/4)+t_bot*exp(complex(0, (-kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(1/4)+t_bot*exp(complex(0, (-ky*lat_constant/sqrt(3))))
    Ham[0][3] = t_parallel*exp(complex(0, (kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(sqrt(3)/4)-t_parallel*exp(complex(0, (-kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(
        sqrt(3)/4)-t_bot*exp(complex(0, (kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(sqrt(3)/4)+t_bot*exp(complex(0, (-kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(sqrt(3)/4)

    Ham[1][0] = 0
    Ham[1][1] = lmd
    Ham[1][2] = Ham[0][3]
    Ham[1][3] = t_parallel*exp(complex(0, (kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(1/4)+t_parallel*exp(complex(0, (-kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(1/4)+t_bot*exp(complex(
        0, (kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(3/4)+t_bot*exp(complex(0, (-kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(3/4)+t_parallel*exp(complex(0, (-ky*lat_constant/sqrt(3))))

    Ham[2][0] = Ham[0][2].conjugate()
    Ham[2][1] = Ham[1][2].conjugate()
    Ham[3][0] = Ham[0][3].conjugate()
    Ham[3][1] = Ham[1][3].conjugate()

    Ham[2][2] = -lmd
    Ham[2][3] = 0
    Ham[3][2] = 0
    Ham[3][3] = -lmd

    e, w = linalg.eig(Ham)
    return e, w



def wf(kx, ky, n):
    e, w = H(kx, ky)
    wf = w[:, argsort(real(e))[n]]
    return wf


dkx = 0.00000001
dky = 0.00000001


def Ax(kx, ky, n):
    return dot(wf(kx, ky, n).transpose().conj(), (wf(kx+dkx, ky, n)-wf(kx, ky, n))/dkx)


def Ay(kx, ky, n):
    return dot(wf(kx, ky, n).transpose().conj(), (wf(kx, ky+dky, n)-wf(kx, ky, n))/dky)


def F(kx, ky, n):
    F = (Ay(kx+dkx,ky,n)-Ay(kx,ky,n))/dkx - (Ax(kx,ky+dky,n)-Ax(kx,ky,n))/dky
    return F


####6 K points to scale the area of 1st BZ######
k1 = [ 2.10067619e+00,  3.63847790e+00]
k2 = [ 4.19506920e+00, -3.62759873e-03]
k3 = [ 2.10067619e+00, -3.63122270e+00]
k4 = [-2.10067619e+00, -3.63845613e+00]
k5 = [-4.19506920e+00,  3.62759873e-03]
k6 = [-2.10067619e+00,  3.63122270e+00]


def line(a, b):
    x1 = a[0]
    y1 = a[1]
    x2 = b[0]
    y2 = b[1]
    s = (y1-y2)/(x1-x2)
    b = (x2*y1-x1*y2)/(x2-x1)
    M = [s, b]
    return M


s1, b1 = line(k1, k6)
s2, b2 = line(k1, k2)
s3, b3 = line(k5, k6)

s4, b4 = line(k2, k3)
s5, b5 = line(k3, k4)
s6, b6 = line(k4, k5)

ddkx = 0.005*2*pi
ddky = 0.005*2*pi


def C(n):
    c = 0
    aaa=0
    for kx in arange(-4.19506920e+00, 4.19506920e+00,ddkx):
        for ky in arange(-3.63122270e+00,3.63847790e+00,ddky):
            if ky < s1*kx+b1 and ky < s2*kx+b2 and ky < s3*kx+b3 and ky > s4*kx+b4 and ky > s5*kx+b5 and ky > s6*kx+b6:
                c = c+F(kx, ky, n)*ddkx*ddky
                aaa=aaa+1
                # print(aaa)   #用来测试步数             
    c = c/2/pi/1.j
    return c
print(C(0))
print(C(1))
print(C(2))
print(C(3))


'''这个模型计算得到的陈数为0'''