1. 文献分享
  2. 物理模型

文献模拟：二维蜂窝晶格px,y轨道的谷对比物理（二）

Written by Posted on Less than 0 min read

上一篇文章详细推导了XYH模型的哈密顿量，下面我们来用程序重复一下它的结果。

我们使用jupyter软件编写python程序，方便展示结果和解释说明

首先导入sympy模块，这是python符号库，可以用于符号型的数学计算

上一篇文章推导的时候发现了点问题，所有的矢量都是在笛卡尔坐标下的，所以应该把2pi去掉，每一项后面再乘以晶格常数，我就懒得改了，这里说明一下
from sympy import *
init_printing(use_latex='mathjax')

定义一些符号，a为晶格常数，t_parallel为头碰头跃迁系数，t_bot为肩并肩跃迁系数，kx和ky为倒格矢，lmd为在位能项

## symbols
a = Symbol("a", positive=true, real=true)
d1, d2, d3, d4 = symbols("d1,d2,d3,d4")
t_parallel = Symbol("t_\parallel", real=true)   
t_bot = Symbol("t_\bot", real=true)    
kx = Symbol("k_x", real=true)
ky = Symbol("k_y", real=true)
lmd = Symbol("lambda", real=true)

定义哈密顿矩阵中的项

H_13=t_parallel*exp(I*2*pi*(kx*1/2+ky*sqrt(3)/6))*(3/4)+t_parallel*exp(I*2*pi*(-kx*1/2+ky*sqrt(3)/6))*(3/4)+t_bot*exp(I*2*pi*(kx*1/2+ky*sqrt(3)/6))*(1/4)+t_bot*exp(I*2*pi*(-kx*1/2+ky*sqrt(3)/6))*(1/4)+t_bot*exp(I*2*pi*(-ky/sqrt(3)))

H_14=t_parallel*exp(I*2*pi*(kx*1/2+ky*sqrt(3)/6))*(sqrt(3)/4)-t_parallel*exp(I*2*pi*(-kx*1/2+ky*sqrt(3)/6))*(sqrt(3)/4)-t_bot*exp(I*2*pi*(kx*1/2+ky*sqrt(3)/6))*(sqrt(3)/4)+t_bot*exp(I*2*pi*(-kx*1/2+ky*sqrt(3)/6))

H_23=H_14

H_24=t_parallel*exp(I*2*pi*(kx*1/2+ky*sqrt(3)/6))*(1/4)+t_parallel*exp(I*2*pi*(-kx*1/2+ky*sqrt(3)/6))*(1/4)+t_bot*exp(I*2*pi*(kx*1/2+ky*sqrt(3)/6))*(3/4)+t_bot*exp(I*2*pi*(-kx*1/2+ky*sqrt(3)/6))*(3/4)+t_parallel*exp(I*2*pi*(-ky/sqrt(3)))

H_1=Matrix([
[lmd,0],
[0,lmd]
])

H_2=Matrix([
[H_13,H_14],
[H_23,H_24]
])


H_3=H_2.conjugate()

H_4=Matrix([
[-lmd,0],
[0,-lmd]
])

将哈密顿量显示出来

H=Matrix([
[H_1,H_2],
[H_3,H_4]
])
H

效果如下，由于显示不全，可自行尝试：

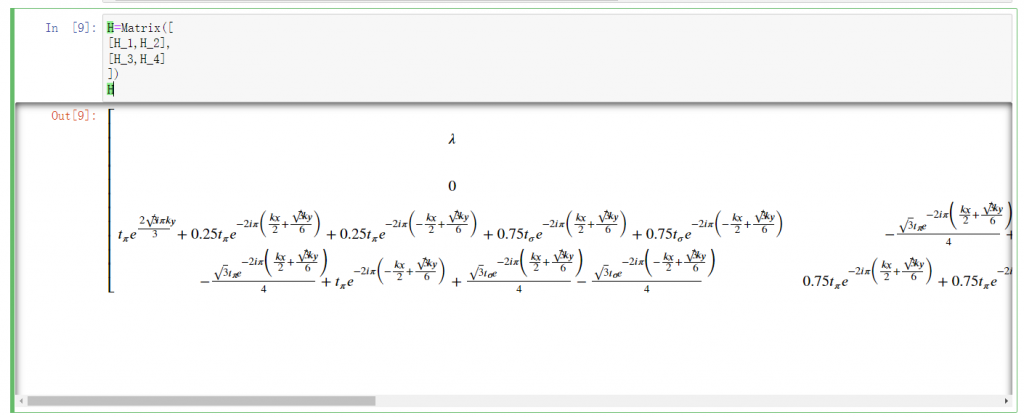
注意这里用的都是分数坐标，不要和vasp的KPOINTS混用，不然拟合不出来！！！

重新写程序，求解这一个4*4矩阵的九期方程，并且代入k点坐标：

from math import *
import math
import sys

from numpy import *

import matplotlib.pyplot as pl

# init K vector of random value

num = 4
knum = 241

lat_constant=1

Ham = [[0 for i in range(num)] for j in range(num)]

# print Ham
# exit()

lmd = 0.4
t_bot = 0.8
t_parallel = -0.02


def H(kx, ky):
    # lattice
    Ham[0][0] = lmd
    Ham[0][1] = 0
    Ham[0][2] = t_parallel*exp(complex(0, (kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(3/4)+t_parallel*exp(complex(0, (-kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(3/4)+t_bot*exp(complex(0, (kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(1/4)+t_bot*exp(complex(0, (-kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(1/4)+t_bot*exp(complex(0, (-ky*lat_constant/sqrt(3))))
    Ham[0][3] = t_parallel*exp(complex(0, (kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(sqrt(3)/4)-t_parallel*exp(complex(0,(-kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(sqrt(3)/4)-t_bot*exp(complex(0, (kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(sqrt(3)/4)+t_bot*exp(complex(0, (-kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(sqrt(3)/4)

    Ham[1][0] = 0
    Ham[1][1] = lmd
    Ham[1][2] = Ham[0][3]
    Ham[1][3] = t_parallel*exp(complex(0, (kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(1/4)+t_parallel*exp(complex(0, (-kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(1/4)+t_bot*exp(complex(0, (kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(3/4)+t_bot*exp(complex(0, (-kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(3/4)+t_parallel*exp(complex(0, (-ky*lat_constant/sqrt(3))))

    Ham[2][0] = Ham[0][2].conjugate()
    Ham[2][1] = Ham[1][2].conjugate()
    Ham[3][0] = Ham[0][3].conjugate()
    Ham[3][1] = Ham[1][3].conjugate()

    Ham[2][2] = -lmd
    Ham[2][3] = 0
    Ham[3][2] = 0
    Ham[3][3] = -lmd

    e, w = linalg.eig(Ham)
    e = [real(e[y]) for y in range(num)]
    e = sort(e)
    return e
    # for y in range(num):
    #     print real(e[y])
# H(0.01,0.03)
# exit()

ens = zeros((num, knum), dtype=float64)
a1 = open("kpoints1", 'r+')
for m in range(knum):
    Kq = a1.readline().strip().split()
    kx,ky=[float(Kq[n]) for n in range(2)]
    e=H(kx,ky)
    for y in range(num):
      ens[y, m] = real(e[y])
print(ens)


pl.figure(figsize=(16.0, 12.4))
pl.subplots_adjust(wspace=0.35)
pl.ylim(-4, 4)
pl.xlim(0, knum)
pl.grid(True)

# print(nOrbits)
for i in range(num):
    # print i
    # pl.plot(ens[i], 'go', ms=5, mew=1)
    pl.plot(ens[i], 'go', ms=5, mew=1)
    # pl.plot(evals[i], 'ro', ms=5, mew=1)
pl.title(r'$\Gamma$')

pl.ylabel("Energy")


pl.show()

print('Done.\n')

这里的k点路径对应文章中的路径，这里我们要用程序将k点分数坐标转换为笛卡尔坐标：

from re import U
import matplotlib.pyplot as pl
from numpy import *

knum=241

lat=matrix([[1.0,0.0,0],[-0.5,sqrt(3.0)/2.0,0],[0,0,20]])


# print(lat,xx)
# exit()

unitI=matrix([[1,0,0],[0,1,0],[0,0,1]])

lat_k=2*pi*unitI*linalg.inv(transpose(lat))


print("this is",lat_k)
# exit()
lat_k=lat_k.A
ens = zeros((knum,3), dtype=float64)
a = open("KPOINTS", 'r+')
for m in range(knum):
    Kq = a.readline().strip().split()
    kx, ky,kz = [float(Kq[n]) for n in range(3)]
    ens[m][0]=kx*lat_k[0][0]+ky*lat_k[1][0]+kz*lat_k[2][0]
    ens[m][1]=kx*lat_k[0][1]+ky*lat_k[1][1]+kz*lat_k[2][1]
    ens[m][2]=kx*lat_k[0][2]+ky*lat_k[1][2]+kz*lat_k[2][2]
print(ens)

画出能带后，效果如下：

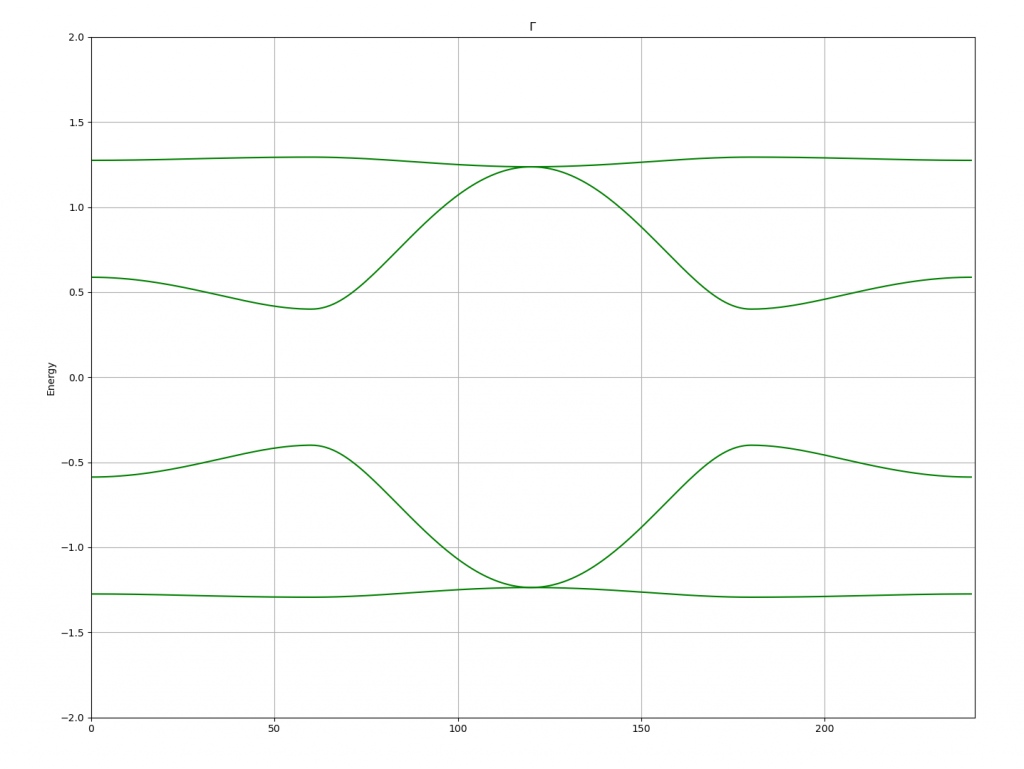
接下来文章中考虑了自旋轨道耦合项，其中γ为自旋轨道耦合的强度，Sy是泡利矩阵，加了soc之后的哈密顿如下：

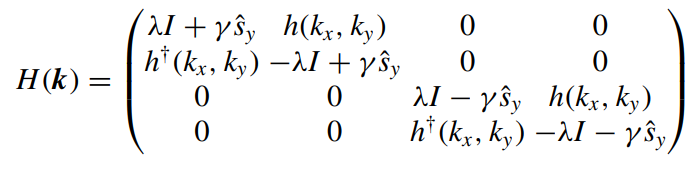
修改程序代码，重新解哈密顿量：

from math import exp
import sys

from numpy import *

import matplotlib.pyplot as pl

# init K vector of random value

num = 8
knum = 241

# print Ham
# exit()
lat_constant=1
lmd = 0.4
t_bot = 0.8
t_parallel = -0.02
gam=0.06

Ham = [[0 for i in range(num)] for j in range(num)]


Ham_soc = [[0 for i in range(num)] for j in range(num)]


def H_soc(kx,ky):
    

    Ham_soc[0][0]=lmd
    Ham_soc[0][1]=complex(0,-gam)
    Ham_soc[1][0]=complex(0,gam)
    Ham_soc[1][1]=lmd

    Ham_soc[0][2]=t_parallel*exp(complex(0, -(kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(3/4)+t_parallel*exp(complex(0, -(-kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(3/4)+t_bot*exp(complex(0, -(kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(1/4)+t_bot*exp(complex(0, -(-kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(1/4)+t_bot*exp(complex(0, -(-ky*lat_constant/sqrt(3))))
    Ham_soc[0][3]=t_parallel*exp(complex(0, -(kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(sqrt(3)/4)-t_parallel*exp(complex(0,-(-kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(sqrt(3)/4)-t_bot*exp(complex(0, -(kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(sqrt(3)/4)+t_bot*exp(complex(0, -(-kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(sqrt(3)/4)
    Ham_soc[1][2]=Ham_soc[0][3]
    Ham_soc[1][3]=t_parallel*exp(complex(0, -(kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(1/4)+t_parallel*exp(complex(0, -(-kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(1/4)+t_bot*exp(complex(0, -(kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(3/4)+t_bot*exp(complex(0, -(-kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(3/4)+t_parallel*exp(complex(0, -(-ky*lat_constant/sqrt(3))))

    Ham_soc[2][0]=conj(Ham_soc[0][2])
    Ham_soc[2][1]=conj(Ham_soc[1][2])
    Ham_soc[3][0]=conj(Ham_soc[0][3])
    Ham_soc[3][1]=conj(Ham_soc[1][3])

    Ham_soc[2][2]=-lmd
    Ham_soc[2][3]=complex(0,-gam)
    Ham_soc[3][2]=complex(0,gam)
    Ham_soc[3][3]=-lmd



    Ham_soc[0+4][0+4]=lmd
    Ham_soc[0+4][1+4]=complex(0,gam)
    Ham_soc[1+4][0+4]=complex(0,-gam)
    Ham_soc[1+4][1+4]=lmd

    Ham_soc[4][6]=t_parallel*exp(complex(0, -(kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(3/4)+t_parallel*exp(complex(0, -(-kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(3/4)+t_bot*exp(complex(0, -(kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(1/4)+t_bot*exp(complex(0, -(-kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(1/4)+t_bot*exp(complex(0, -(-ky*lat_constant/sqrt(3))))
    Ham_soc[0+4][3+4]=t_parallel*exp(complex(0, -(kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(sqrt(3)/4)-t_parallel*exp(complex(0,-(-kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(sqrt(3)/4)-t_bot*exp(complex(0, -(kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(sqrt(3)/4)+t_bot*exp(complex(0, -(-kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(sqrt(3)/4)
    Ham_soc[1+4][2+4]=Ham_soc[0][3]
    Ham_soc[1+4][3+4]=t_parallel*exp(complex(0, -(kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(1/4)+t_parallel*exp(complex(0, -(-kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(1/4)+t_bot*exp(complex(0, -(kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(3/4)+t_bot*exp(complex(0, -(-kx*lat_constant*1/2+ky*lat_constant*sqrt(3)/6)))*(3/4)+t_parallel*exp(complex(0, -(-ky*lat_constant/sqrt(3))))

    Ham_soc[2+4][0+4]=conj(Ham_soc[0+4][2+4])
    Ham_soc[2+4][1+4]=conj(Ham_soc[1+4][2+4])
    Ham_soc[3+4][0+4]=conj(Ham_soc[0+4][3+4])
    Ham_soc[3+4][1+4]=conj(Ham_soc[1+4][3+4])

    Ham_soc[2+4][2+4]=-lmd
    Ham_soc[2+4][3+4]=complex(0,gam)
    Ham_soc[3+4][2+4]=complex(0,-gam)
    Ham_soc[3+4][3+4]=-lmd

    e, w = linalg.eig(Ham_soc)
    e = [real(e[y]) for y in range(num)]
    e = sort(e)
    print(e)
    return e


ens = zeros((num, knum), dtype=float64)
a1 = open("kpoints1", 'r+')
for m in range(knum):
    Kq = a1.readline().strip().split()
    kx,ky=[float(Kq[n]) for n in range(2)]
    e=H_soc(kx,ky)
    for y in range(num):
        ens[y, m] = real(e[y])
print(ens)

pl.figure(figsize=(16.0, 12.4))
pl.subplots_adjust(wspace=0.35)
pl.ylim(-2, 2)
pl.xlim(0, knum)
pl.grid(True)

# print(nOrbits)
for i in range(num):
    # print i
    # pl.plot(ens[i], 'go', ms=5, mew=1)
    pl.plot(ens[i], 'g-', ms=5, mew=1)
    # pl.plot(evals[i], 'ro', ms=5, mew=1)

# pl.plot(ens[4], 'go', ms=5, mew=1)
pl.title(r'$\Gamma$')

pl.ylabel("Energy")

# my_array = wf_array(my_model, [41, 41, 2])

# my_array.solve_on_grid([-0.5, -0.5, 0])

# for i in range(nOrbits):
#     curv_a_1 = my_array.berry_flux([i])
#     print "%d C= %f" % (i+1, curv_a_1[0]/np.pi/2.0)

pl.show()

print('Done.\n')

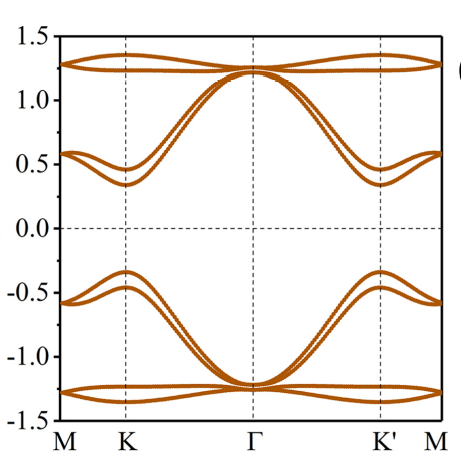
加soc后效果如下：

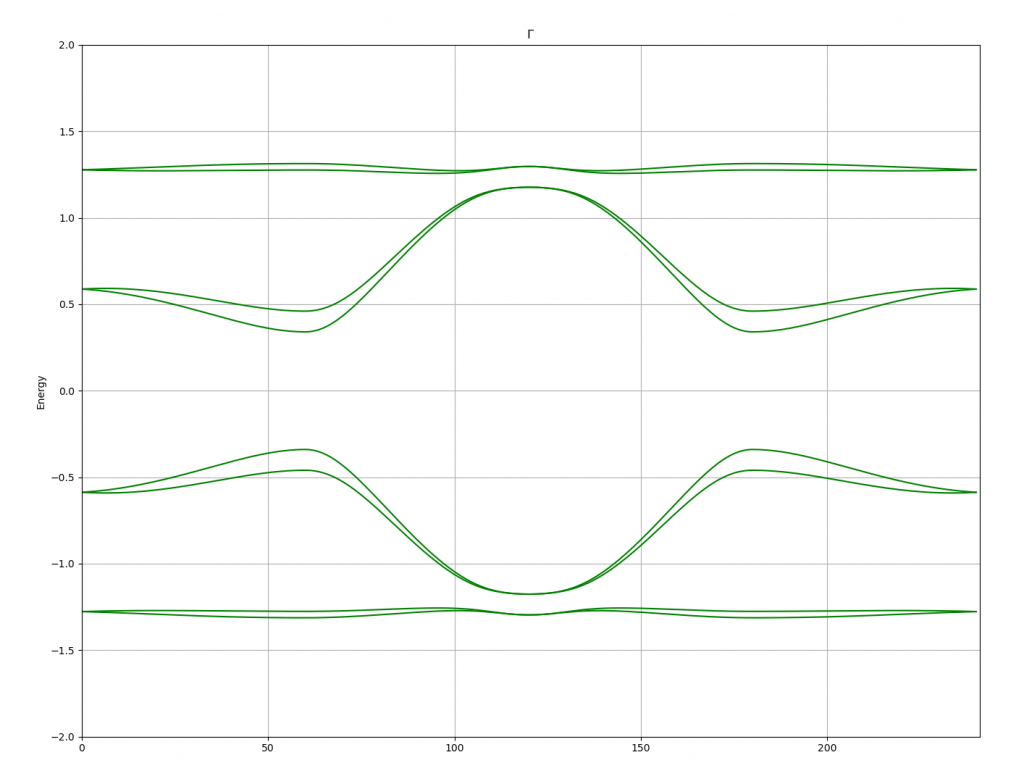
对比文章

所有的代码放在了下面的压缩包中，可供下载

XYH模型下载

Related articles

Next
No Comments
Leave a comment Cancel
Comments to: 文献模拟：二维蜂窝晶格px,y轨道的谷对比物理（二）

您的邮箱地址不会被公开。 必填项已用 * 标注