杨氏模量与泊松比

使用的公式如下：

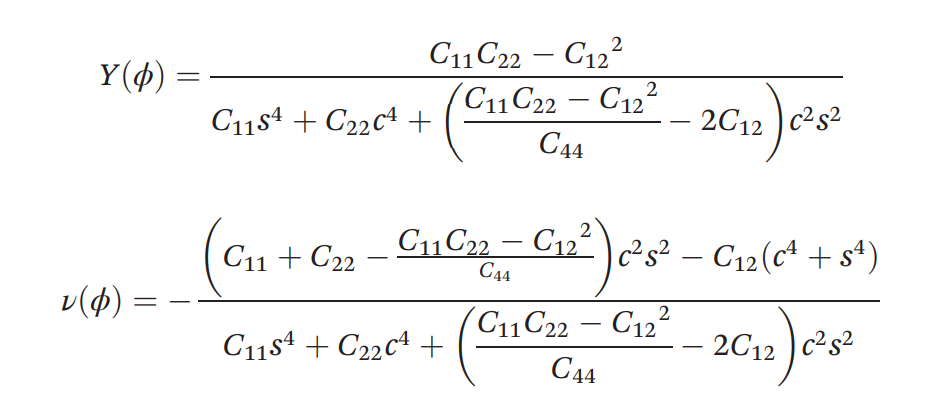
import matplotlib.pyplot as pl

import numpy as np

import math

C_11=190.09

C_12=96.06

C_22=190.09

C_44=33.02



# C_11=138.89

# C_12=68.63

# C_22=202.73

# C_44=77.89





theta=np.arange(0,2*np.pi,0.02)

# print(theta[0])

a=0

for i in theta:

    a=a+1

ym=np.zeros(a)



for i in range(0,a):

    ym[i]=(C_11*C_22-C_12**2)/(C_11*math.sin(theta[i])**4+C_22*math.cos(theta[i])**4+((C_11*C_22-C_12**2)/C_44-2*C_12)*math.cos(theta[i])**2*math.sin(theta[i])**2)



po=np.zeros(a)

for i in range(0,a):

    po[i]=  -( ((C_11+C_22-(C_11*C_22-C_12**2)/C_44)*math.cos(theta[i])**2*math.sin(theta[i])**2)-C_12*(math.sin(theta[i])**4+math.cos(theta[i])**4) )  /  (C_11*math.sin(theta[i])**4+C_22*math.cos(theta[i])**4+((C_11*C_22-C_12**2)/C_44-2*C_12)*math.cos(theta[i])**2*math.sin(theta[i])**2)





ax1= pl.subplot(121, projection='polar')

ax1.plot(theta, ym, linewidth=3,color='red')

ax1.grid(True) #是否有网格



ax2= pl.subplot(122, projection='polar')

ax2.plot(theta, po, linewidth=3,color='red')

ax2.grid(True) #是否有网格



pl.show()